[Leet code] 2943. Maximize Area of Square Hole in Grid

문제 링크 : https://leetcode.com/problems/maximize-area-of-square-hole-in-grid/description/?envType=daily-question&envId=2026-01-15

문제 설명

입력으로 n, m, hBars, vBars 가 주어진다.

n, m 은 각각 제시된 직사각형이 가질 수 있는 최대 수평선의 개수와 최대 수직선의 개수이다. 

hBars , vBars 는 각각 제거할 수 있는 수평선의 개수와 수직선의 개수이다. 

 

n,m 으로 구성된 최대 직사각형에서 hBars, vBars 중 일부를 제거 (제거하지 않아도 됨) 하여 만들수 있는 최대 정사각형의 면적을 구하는 문제다. 설명은 어려워도 예시를 보면 이해가 간다. 

 

Example 1:

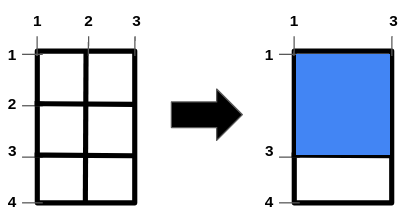
Input: n = 2, m = 1, hBars = [2,3], vBars = [2]

Output: 4

Explanation:

The left image shows the initial grid formed by the bars. The horizontal bars are [1,2,3,4], and the vertical bars are [1,2,3].

One way to get the maximum square-shaped hole is by removing horizontal bar 2 and vertical bar 2.

Example 2:

Input: n = 1, m = 1, hBars = [2], vBars = [2]

Output: 4

Explanation:

To get the maximum square-shaped hole, we remove horizontal bar 2 and vertical bar 2.

 

오랜만에 만난 재밌는 수학문제 :) 

문제 풀이 

최대한 큰 정사각형을 만들고자 한다면 최대한 연속된 개수의 수평선과 수직선을 제거해야한다. 

일단 hBars 와 vBars 를 정렬하여 연속된 수평선과 수직선이 몇개나 제시되었는지를 확인한다. 

가장 긴 연속된 수평선과 수직선의 개수를 구한다음 둘중에 더 작은 수 r 을 구한다.

(연속된 수평선 3개, 수직선이 2개있을 경우 해당 선을 모두 제거해도 수직선 2개를 제거한것 보다 큰 정사각형은 구할 수 없기 때문이다 ) 

만들 수 있는 최대면적은 ( r + 1 )^2 이 된다. 

(직선 한개를 제거한 경우 변의 길이는 제거한 선분 + 1 이 되기 때문)

 

코드 (Rust)

use std::cmp;
impl Solution {
    pub fn maximize_square_hole_area(n: i32, m: i32, h_bars: Vec<i32>, v_bars: Vec<i32>) -> i32 {
        let (mut h_bars, mut v_bars) = (h_bars, v_bars);
        
        h_bars.sort_unstable();
        v_bars.sort_unstable();
      
        let h_max = Self::get_max(&h_bars);
        let v_max = Self::get_max(&v_bars);
       
        let side = cmp::min(h_max, v_max) + 1;
        side * side
    }

    fn get_max(bars: &[i32]) -> i32 {
        let mut max_cnt = 1;
        let mut cur_cnt = 1;
       
        for w in bars.windows(2) {
            if w[1] == w[0] + 1 {
                cur_cnt += 1;
            } else {
                cur_cnt = 1;
            }
            max_cnt = cmp::max(max_cnt, cur_cnt);
        }
        max_cnt
    }
}